Low Volatility Casinos
Low Volatility: The Case of the Grind Joints Casinos
The opposite of the casinos that deal to high rollers are the grind joints.
They acquired their name by earning their casino win from small bets with large volumes.
These casinos generally feature a large number of slot machines with lower denominations and low limit table games.
To be successful, these casinos must have a large number of players that collectively have a large volume of small bets.
A benefit of this approach is consistency in actual win rate. For the opposite reason, that high rollers cause high volatility, low rollers create low volatility.
This is because of the law of large numbers, which dictates that the more bets made, the closer the proportion of money wagered retained by the casino will be to the house advantage. Therefore, grind joints should realize actual win rates that more consistently approach the theoretical win rate than casinos that cater to premium customers. Of course, the challenge to the grind joints becomes to insure that they handle the volume of bets necessary to produce net gaming revenues sufficient to pay expenses and taxes and make a profit.
Casino Games Blog 2024
The Bitcoin Casino Guide
- Bonus Amount: $3,000 up to $10,000. The best daily bonuses on the internet.
- Games: An incredible number of slots, table games, and video pokers, including HTML5 games.
- Strong security protocols of 128-bit encryption
- Audited and guaranteed fair by TST
- Website: https://www.lasvegasusa.eu/casino/
- Established: 1999
- Software: Real Time Gaming (RTG)
- US and Canadians players supported
- Platforms Supported: Windows, Mac, iPhone, iPad, & Android.
- Type of Casino: Online & Instant or download.
- Free Slots Games: Yes
- Customer Support: 24/7 live chat support, as well as a toll-free phone number: +506-283-0061, and e-mail support
Write your review of Las-Vegas USA Casino
- Website: http://www.royalacecasino.eu
- Casino Type: download client, instant play, and mobile
- Software: Real Time Gaming (RTG)
- Owner: Emoney Processing Casinos LTD
- Established: 2009
- Casino Promotion: 100% Match Deposit Bonus up to $4,000, Daily and Weekly Bonuses
- Coupon Code: CASINO400
- Currencies: US$, Euros, Yen, Pounds, Bitcoin
- Mobile: both desktop and mobile compatibility
- VIP Program: 5 levels Available
- Support: World Class Support, 24/7 live chat & Toll-free phone number for USA and Canada
- Security: 128-bit SSL encryption
- Certified by: CDS (Central Disputes System)
- Languages: English
- License: Costa Rica
Write your review of Royal Ace Casino
- Bonus: 400% up to $10,000.
- Website: https://www.sunpalacecasino.eu/
- Software: Real Time Gaming (RTG)
- Deposit Methods: ClickandBuy, MasterCard, Money Order, Neteller, Visa Electron, instaDebit, Visa, MST Gift Card, Skrill, Bitcoin
- Withdrawal Methods: ACH, Cheque, Money Order, Neteller, Skrill
- Withdrawal Times: EWallets: 2-5 days, Credit / Debit Cards: 10-12 days, Bank Transfers: 7-12 days, Cheques: 21-28 days
- Pending Time: 3-7 days
- Withdrawal Limit: $5,000 per week
- Games: Incredible number of games of all types
- support: 24/7 through live chat, phone, or e-mail
- Support Response Time: 24 hours via email or Instant using Live Chat.
- Encryption: 128-bit SSL
- Audited and found fair by TST
- Languages: English.
- Progressive Jackpots: up to Million-Dollar.
- Restricted Countries: Bosnia, Costa Rica, Malaysia, Morocco, Netherlands, Russia.
Write a review of Sun Palace Casino
- Bonus: 320% Bonus + 45 Free Spins
- Casino Website: https://www.silveroakcasino.com/
- Casino Promotion: 320% Match Deposit Bonus up to $10,000 in 10 first deposits, up to $100 No Deposit Bonus, Weekly and Monthly Cashback, and much more.
- Casino Type: download client, instant play, mobile, and live dealers
- Software: Real Time Gaming (RTG)
- Live Casino: Available Live Dealers Casino
- Owner: Emoney Processing Casinos LTD
- Established: 2009
- Currencies: US$, Euros, Yen, Pounds, Bitcoin
- Mobile: both desktop and mobile compatibility
- VIP Program: 5 levels Available
- Support: World Class Support, 24/7 live chat & Toll-free phone number for USA and Canada
- Security: 128-bit SSL encryption
- Certified by: CDS (Central Disputes System)
- Languages: English
- License: Costa Rica
Write your review of Silver Oak Casino
- Bonus: First Deposit 350% Bonus + 25 Free Spins
- Website: https://www.planet7casino.com/
- Casino Type: download client, instant play, mobile, and live dealers
- Software: Real Time Gaming (RTG)
- Live Casino: Available Live Dealers Casino
- Owner: Emoney Processing Casinos LTD
- Established: 2008
- Casino Promotion: 200% Match Deposit Bonus up to $4,000, and much more.
- Currencies: US$, Euros, Yen, British Pounds, Bitcoin
- Mobile: both desktop and mobile compatibility
- VIP Program: Available
- Support: World Class Support, 24/7 live chat & Toll-free phone number for USA and Canada
- Security: 256-bit SSL encryption
- Certified by: CDS (Central Disputes System)
- Languages: English
- License: Costa Rica, Cyprus, the United Kingdom, and the Netherlands.
Write a review of Planet 7 Casino
- Bonus: Get 300% Match up to $3000 FREE Welcome Bonus
- Website: https://www.clubworldcasinos.com
- Software: Real Time Gaming (RTG)
- Mobile: Android, iPhone, iPad
- Casino Type: Download, Instant Play, Mobile
- Currency: US dollars
- Language: English
- License: Curacao
- Owner: Club World Casinos Group Casinos
- Established: 2005
- Audit: RTP Not publicly audited
- Currency: US dollars
Write a review of Club World Casino
- Bonus: Get 300% Match up to $3000 FREE Welcome Bonus
- Website: https://vegascasinoonline.eu/
- Established: 1999
- Software: Real Time Gaming (RTG)
- Currencies: US$
- US and Canadians players: supported
- Bonus Amount: up to $11,000 Match Bonus
- Platforms Supported: Windows, Mac, iPhone, iPad, & Android.
- Type of Casino: Download & Online Instant Play.
- Free Slots Games: Yes
- Owner: Main Street Vegas Group Casinos
- License: Costa Rica
- US Customer Support: (877) 691-5124
- Canada Customer Support: (888) 387-6717
- Email Address: [email protected]
- Live Chat: Yes
- Response Time: 24 hours via email or Instant using Live Chat.
- Languages: English.
- Progressive Jackpots: up to 1 Million-Dollar.
Write a review of Vegas Casino Online
Gambler's Ruin, Volatility, and the Freeze-Out
The probabilities of each side winning a freeze-out played to completion can be computed using a “gambler’s ruin” model.
The general version of this problem can be stated as follows:
A gambler starts off with $a and plays against an adversary who has $(n−a) > 0.
The plays are independent and at each play, the gambler wins $1 goes with probability p and loses $1 with probability q = 1−p.
Play continues until one of the two players go broke, so that the winning player ends up with $n.
What is the probability of the gambler’s ultimate ruin, and what is the probability of the gambler’s ultimate success?
Letting r = q/p, these two probabilities are given by:
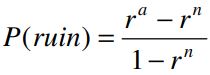
and
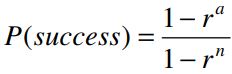
if p ≠ q
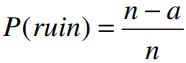
and
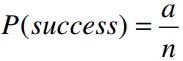
if p = q
Probability of Winning
As an example, suppose a player enters a casino with $100 and makes $1 color bets in roulette until winning $20 or going broke, whichever happens first.
The gambler’s ruin model can be applied as though the casino is the adversary who will go broke after a loss of $20.
From the gambler’s point of view, the probability of winning a color bet is 18/38 and probability of losing is 20/38. Hence, a = 100, n = 120, p = 18/38, q = 20/38, and r = 20/18, or about 1.1111. The probability of ruin before winning $20 is:
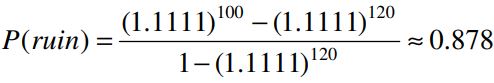
This means the probability of winning $20 before losing all $100 is about 0.122.
If the same gambler chooses to play the pass line (only) at craps, with a slightly higher p ≈ .493, then the probability of winning $20 before going broke increases dramatically to 0.556. For a fair game, where p = .5, the probability of the $100- bankroll player winning $20 before ruin is 0.833. These examples show that for values of p not too far from .5, a small shift in the probability of winning a single play can have a considerable impact on the probability of ruin.
A special case of the gambler’s ruin problem that can be applied to the freeze-out game results when the gambler will play until either doubling the initial $a bankroll or going broke.
This version can be formally stated as follows:
A gambler starts with $a, and on each of a series of independent wagers wins $1 with probability p and loses $1 with probability q = 1−p.
The game continues until the gambler either doubles the initial $a, or loses it all and is ruined.
Analogous to the example above, apply the gambler’s ruin model as though the casino will go broke after the gambler doubles the $a. Noting that n = 2a for this “double or nothing” version, after a little algebra the following probabilities of ruin and success can be obtained from the formulas for the general model:
and
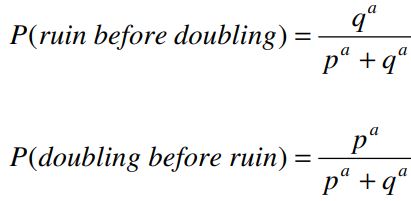
These formulas assume each play results in the winning or losing of one unit and that the gambler will quit if the initial capital is doubled. If a is large, then when p>q, the probability the (advantaged) gambler is ruined before doubling is about equal to (q/p)a, the formula for the probability of ultimate ruin if the gambler plays forever (i.e., does not stop if the initial capital is doubled). If p<q, the probability that the (disadvantaged) gambler is ruined before doubling is about 1−(p/q)a, for large a.
Gambler’s ruin . . .
This is the simple proposition that all other things being equal, the gambler with more money in a bust out game, i.e., where play continues until you win or lose all your money, is more likely to prevail over the gambler with less money.
Of course, casinos not only have more money than almost all players, they also possess a house advantage to assure that all things are not equal.
Gambler’s Ruin – Government Style
The concept is simple enough.
If the government imposes a limit on how much a person can gamble on each wager, then the potential amount that that person can lose in a given amount of time also is limited.
This is the logic behind the $5 per hand bet limitation imposed in Colorado and elsewhere.
The problem, however, is that the likelihood that a person will come out a winner decreases as the number of wagers increases.
Take three gamblers each playing roulette, betting even money propositions and each with a $200 bankroll that they intend to play until they lose it all or double it.
The first player bets $200 and has a 47.4% chance of winning $200 before losing $200.
This is because on just one spin of the wheel he will either lose the entire $200, or win and double his bankroll.
The second player bets $25 per hand and has a 30.1% of winning $200 before losing $200.
The third player with a $5 bet limit has only a 1.5% of winning $200 before losing $200. The results are similar for other games.
Was This Helpful?
Recommend us on Facebook
Bitcoin Casinos
Online Casinos in The USA
Online Casinos in the UK