- The Reviews
- UNIBET Review 2026
- MANSION Review 2026
- BETSAFE Review 2026
- BWIN Review 2026
- BETSSON Review 2026
- JETBULL Review 2026
- WILLIAM HILL Review 2026
- BET-AT-HOME Review 2026
- ZET Casino Review 2026
- CASINO.com Review 2026
- Mr GREEN Review 2026
- 888 Review 2026
- VEGAS CASINO ONLINE Review 2026
- LAS-VEGAS USA Casino Review 2026
- SUN PALACE Casino Review 2026
- ROYAL ACE Casino Review 2026
- PLANET 7 Casino Review 2026
- CLUB WORLD Casino Review 2026
- SILVER OAK Casino Review 2026
- Free Casino Games
US
- Best Online Casino Games Guide
- Choose Your Best Online Casino
- The Best Casino Games
- Online Card Games
- Best Online Machine Games
- Table Games
- Online Slots
- Complete Modern Online Blackjack Guide
- Free Blackjack Basic Strategy
- Simplified Blackjack Playing Strategy
- How to Play Blackjack Online Like Pros
- Advanced Blackjack Rules and Strategy
- Step-by-Step Blackjack Playing Procedures
- Blackjack Playing Options Guide
- Master Blackjack Card Counting
- Modern Blackjack Card Counters Challenge
- Which is the Best Blackjack Betting System?
- Nine-Count Blackjack Strategy Review
- Blackjack Myths and Errors
- Online Roulette
- Sportsbook
- Online Poker
- Online Video Poker
- Online Scratch Cards
- Online Bingo
- Online Baccarat
- Online Craps
- Asian Casino Games
- Online Keno
- Online Sic Bo
- Casino Bonuses
- Online Casino Reviews
- UNIBET Review, Casino, Sportsbook, Poker & Live Dealers
- BETSAFE Review, Casino, Poker, Live Dealers & Sportsbook
- MANSION Review, Casino, Sportsbook & Live Dealers
- BWIN Review, Sportsbook, Casino, Poker & Live Dealers
- BETSSON Review, Sportsbook, Casino, Live Dealers, Poker
- JETBULL Review -Casino, Sportsbook, Live Dealers
- BET_AT_HOME Review, Sportsbook, Casino, Poker, Live Dealers
- WILLIAM HILL Review -Casino, Sportsbook, Live Dealers, Poker
- ZET Casino Review
- Mr GREEN Review -Casino, Sportsbook & Live Dealers
- CASINO.com Review -Online Casino & Live Dealers
- Las-Vegas USA Casino Review
- Sun Palace Casino Review
- Royal Ace Casino Review
- Planet 7 Casino Review
- Club World Casino Review
- Vegas Casino Online Review
- Silver Oak Casino Review
- Free Casino Games
The Slots Machines Random Number Generator - Can a Machine Be Random?
Technically, a machine cannot be random. Slot machines, in fact, are “pseudo”-random. All physical events are deterministic or caused by something.
Mechanical randomizers such as bingo balls, roulette wheels, and dice use the laws of physics to maximize uncertainty. The basis of all random-like events is a combination of complex or nonlinear relationships and initial uncertainty.
A roulette wheel spins in one direction and the ball is thrown in the opposite, so there are a huge number of possible paths that the ball could follow around the wheel. The roulette wheel is complex. Nonetheless, it would still be possible to predict where the ball was going to land (which path it would take) if you knew exactly how much effort was put into throwing it and where exactly the ball was relative to the wheel when it was thrown.
The fact that we cannot control or measure exactly how much energy is put into throwing the ball means that the outcome of the roulette wheel is essentially random.
In fact, we cannot measure anything exactly. The combination of complexity and uncertainty produces chaos, and chaos is the basis for randomness.
Scientists used to believe that error in measurement only had a trivial effect on prediction, but the study of chaos has shown that a little error when measuring something complex can lead to complete uncertainty and a fundamental inability to predict.
Slot machines are computers, and computers are inherently complex, but they are not uncertain. Slot machines use a random number generator (RNG) to create an erratic sequence of numbers. If the right values are selected for the RNG, the sequence will be virtually unpredictable.
- Bonus Amount: $3,000 up to $10,000. The best daily bonuses on the internet.
- Games: An incredible number of slots, table games, and video pokers, including HTML5 games.
- Strong security protocols of 128-bit encryption
- Audited and guaranteed fair by TST
- Website: https://www.lasvegasusa.eu/casino/
- Established: 1999
- Software: Real Time Gaming (RTG)
- US and Canadians players supported
- Platforms Supported: Windows, Mac, iPhone, iPad, & Android.
- Type of Casino: Online & Instant or download.
- Free Slots Games: Yes
- Customer Support: 24/7 live chat support, as well as a toll-free phone number: +506-283-0061, and e-mail support
Write your review of Las-Vegas USA Casino
- Website: http://www.royalacecasino.eu
- Casino Type: download client, instant play, and mobile
- Software: Real Time Gaming (RTG)
- Owner: Emoney Processing Casinos LTD
- Established: 2009
- Casino Promotion: 100% Match Deposit Bonus up to $4,000, Daily and Weekly Bonuses
- Coupon Code: CASINO400
- Currencies: US$, Euros, Yen, Pounds, Bitcoin
- Mobile: both desktop and mobile compatibility
- VIP Program: 5 levels Available
- Support: World Class Support, 24/7 live chat & Toll-free phone number for USA and Canada
- Security: 128-bit SSL encryption
- Certified by: CDS (Central Disputes System)
- Languages: English
- License: Costa Rica
Write your review of Royal Ace Casino
- Bonus: 400% up to $10,000.
- Website: https://www.sunpalacecasino.eu/
- Software: Real Time Gaming (RTG)
- Deposit Methods: ClickandBuy, MasterCard, Money Order, Neteller, Visa Electron, instaDebit, Visa, MST Gift Card, Skrill, Bitcoin
- Withdrawal Methods: ACH, Cheque, Money Order, Neteller, Skrill
- Withdrawal Times: EWallets: 2-5 days, Credit / Debit Cards: 10-12 days, Bank Transfers: 7-12 days, Cheques: 21-28 days
- Pending Time: 3-7 days
- Withdrawal Limit: $5,000 per week
- Games: Incredible number of games of all types
- support: 24/7 through live chat, phone, or e-mail
- Support Response Time: 24 hours via email or Instant using Live Chat.
- Encryption: 128-bit SSL
- Audited and found fair by TST
- Languages: English.
- Progressive Jackpots: up to Million-Dollar.
- Restricted Countries: Bosnia, Costa Rica, Malaysia, Morocco, Netherlands, Russia.
Write a review of Sun Palace Casino
- Bonus: 320% Bonus + 45 Free Spins
- Casino Website: https://www.silveroakcasino.com/
- Casino Promotion: 320% Match Deposit Bonus up to $10,000 in 10 first deposits, up to $100 No Deposit Bonus, Weekly and Monthly Cashback, and much more.
- Casino Type: download client, instant play, mobile, and live dealers
- Software: Real Time Gaming (RTG)
- Live Casino: Available Live Dealers Casino
- Owner: Emoney Processing Casinos LTD
- Established: 2009
- Currencies: US$, Euros, Yen, Pounds, Bitcoin
- Mobile: both desktop and mobile compatibility
- VIP Program: 5 levels Available
- Support: World Class Support, 24/7 live chat & Toll-free phone number for USA and Canada
- Security: 128-bit SSL encryption
- Certified by: CDS (Central Disputes System)
- Languages: English
- License: Costa Rica
Write your review of Silver Oak Casino
- Bonus: First Deposit 350% Bonus + 25 Free Spins
- Website: https://www.planet7casino.com/
- Casino Type: download client, instant play, mobile, and live dealers
- Software: Real Time Gaming (RTG)
- Live Casino: Available Live Dealers Casino
- Owner: Emoney Processing Casinos LTD
- Established: 2008
- Casino Promotion: 200% Match Deposit Bonus up to $4,000, and much more.
- Currencies: US$, Euros, Yen, British Pounds, Bitcoin
- Mobile: both desktop and mobile compatibility
- VIP Program: Available
- Support: World Class Support, 24/7 live chat & Toll-free phone number for USA and Canada
- Security: 256-bit SSL encryption
- Certified by: CDS (Central Disputes System)
- Languages: English
- License: Costa Rica, Cyprus, the United Kingdom, and the Netherlands.
Write a review of Planet 7 Casino
- Bonus: Get 300% Match up to $3000 FREE Welcome Bonus
- Website: https://www.clubworldcasinos.com
- Software: Real Time Gaming (RTG)
- Mobile: Android, iPhone, iPad
- Casino Type: Download, Instant Play, Mobile
- Currency: US dollars
- Language: English
- License: Curacao
- Owner: Club World Casinos Group Casinos
- Established: 2005
- Audit: RTP Not publicly audited
- Currency: US dollars
Write a review of Club World Casino
- Bonus: Get 300% Match up to $3000 FREE Welcome Bonus
- Website: https://vegascasinoonline.eu/
- Established: 1999
- Software: Real Time Gaming (RTG)
- Currencies: US$
- US and Canadians players: supported
- Bonus Amount: up to $11,000 Match Bonus
- Platforms Supported: Windows, Mac, iPhone, iPad, & Android.
- Type of Casino: Download & Online Instant Play.
- Free Slots Games: Yes
- Owner: Main Street Vegas Group Casinos
- License: Costa Rica
- US Customer Support: (877) 691-5124
- Canada Customer Support: (888) 387-6717
- Email Address: [email protected]
- Live Chat: Yes
- Response Time: 24 hours via email or Instant using Live Chat.
- Languages: English.
- Progressive Jackpots: up to 1 Million-Dollar.
Write a review of Vegas Casino Online
Technical details of the Random Number Generator
It is not essential that you understand how the RNG creates “random” numbers, but the following information is provided here for those who are interested. Essentially, my goal is to demystify the nature of slot machines and random numbers.
The RNG in slots uses Lehmer’s congruential iteration. In this formula, there are three constant values that are usually set as very large numbers: a multiplier
(a) an added number
(b) and a divider also know as the modulus (m). The RNG works as follows.
- Start with a seed number, e.g., time of day.
- Multiply by one number (a) and add another number (b).
- Divide by the modulus (m).
- The remainder is the first random number.
- Translate this into a number in a useful range, e.g., 0 to 1, 1 to 36, 1 to 516, etc.
- Use the remainder as the seed for the next number.
In the Table, we illustrate how this algorithm works with a = 3, b = 5, m = 7, and a starting value (seed) of 12. The values in the Table would not produce a very good series of random numbers, but they do illustrate how the algorithm works.
Seed | Times 3 plus 5 |
| Divide by 7 | Remainder |
12 | 12*3+5 | =41 | 5.857 | 6 |
6 | 6 * 3+5 | =23 | 3.286 | 2 |
2 | 2 * 3+5 | =11 | 1.571 | 4 |
4 | 4 * 3+5 | =17 | 2.429 | 3 |
3 | 3 * 3+5 | =14 | 2.000 | 0 |
0 | 0 * 3+5 | =5 | 0.714 | 5 |
5 | 5 * 3+5 | =20 | 2.857 | 6 |
6 | 6 * 3+5 | =23 | 3.286 | 2 etc. |
The size of the random number will depend on the size of the modulus number. As in the example in the Table, with a modulus of 7, the possible range of the “random” values is from 0 to 6.
The maximum value of the remainder will always be one less than the modulus. The remainder is the raw “random” number. The raw “random” number is translated into a number in a useful range by first dividing it by the modulus number so that it becomes a proportion between 0 and 1.
Given a modulus of 7, a remainder of 2 becomes an RNG value of 2/7 = 0.286. If the programmer would like the final range of RNGs to be between 1 and 36, the proportion is multiplied by 36 and rounded off.
The value 0.286 times 36 is 10.296, which rounds off to 10. This then is the final number, or “stop,” used to determine which image is displayed on the slot machine reel or video screen.
The numbers produced by this procedure are not random, but, if produced by a very large modulus (e.g., a number in the billions) and then translated into a reasonably small range (e.g., 1 to 36 or even 1 to 516), are very erratic and difficult to distinguish from numbers in a sequence produced by pure chance.
Random Versus Pseudorandom
As shown above, the numbers produced by the RNG are not truly random. Mathematicians call them pseudorandom numbers. In fact, it would be a contradiction in terms to compute a random number, because computing means that the number is exactly predictable.
But numbers produced by the RNG are difficult to distinguish from truly random numbers. Most computerized RNGs are good enough for practical purposes. This algorithm can run at an incredibly rapid speed, churning through thousands of pseudorandom numbers per second.
It may be possible in the future that computers will no longer have to rely on Lehmer’s congruential iteration to produce pseudorandom numbers.
Instead, chips may become widely available that rely more directly on chaotic processes such as turbulence to generate truly random numbers. If this is the case, the technology would change a little, but the fact is that slots would still be just as unpredictable.
As stated above, the inherent limitation of a machine is that it cannot create true uncertainty, only complexity. The RNG always follows exactly the same order. The “random” numbers always go through the same sequence or cycle.
If the modulus is a prime number of around four billion, then the sequence will not repeat itself until it has run through about four billion numbers. At that length, assuming a 90% payback percentage and a 25-cent bet per spin, one would lose about $33 million trying to wait for the cycle to repeat itself.
Breaking up the cycle
However, even a cycle that is four billion numbers long would still leave the slot machine vulnerable to a clever (and very rich) player determined to beat the game.
As stated above, to achieve true randomness, you must have both complexity and uncertainty. The congruential iteration provides a great deal of complexity, but no uncertainty. If you know the first number in the sequence, you know exactly what the next number will be.
To add uncertainty, the RNG runs continuously whether or not anyone is playing. The RNG in a slot amchine runs all the time, but most of these numbers are not used. When the spin button is pressed, the current value of the RNG is “polled.” What this means is that the value of the RNG at that millisecond when the spin button is pressed is passed from the RNG to the virtual reel part of the slot program, where the computer calculates which pictures to display.
For a three-reel slot, three numbers are drawn from the RNG and used to determine where to spin the reels. As such, the numbers drawn depend on the exact millisecond when the spin button is pressed. A millisecond later and the outcome of the slot machine will be different.
The player does not know how many RNGs were skipped between one button press and the next. As a result, the outcomes of slot machines are in effect random, so waiting for the cycle to repeat itself is not possible.
To reiterate, only a small percentage of the RNG numbers are actually used by the slot machine: those numbers that it is generating at the millisecond when the player presses the spin button. Therefore, you never know which part of the cycle you are in, so the result is essentially random.
It must be noted that slot machines and other EGMs are designed according to a number of different specifications. In some cases, several different RNGs may be used; in other cases, two RNGs are used (one to determine if the spin will win or lose and another to determine how much to payout).
Details on the implementation of random numbers in slot machine designs can be found by searching through the U.S. patent office’s Web site (http://www.uspto.gov/patft/index.html).
An advanced search using the phrase “slot machine” found 1391 patents since 1976. The design is presented here not to represent all slot machines, but to help the reader understand how an EGM can create a random experience from pseudorandom numbers and provide the player with a varied gambling experience.
Reel weights
The pictures shown on a slot reel do not necessarily correspond directly to the odds of winning. A symbol might occur twice on the reel but only land on the pay line once every 50 spins. This is accomplished through a process called mapping, determined by a computer inside the slot machine. Each stop on the slot machine’s “virtual” reel is equally likely, but more of these virtual reel stops are mapped onto nonpaying symbols (blanks) or low-paying symbols (bars) than onto high-paying symbols (sevens and cherries). Thus, through virtual reel mapping, the outcomes are weighted in favor of low-paying outcomes.
Virtual reel mapping was developed because the number of pictures on the physical reel was limited by the circumference of a reel.
If slot manufacturers did not use virtual reel mapping to weight the pictures on the actual reels, they would only be able to offer small prizes.
A reel with only 20 symbol stops would have only 8000 possible outcomes. Such reels would be limited to fairly small prizes. Varying the probability of different pictures on the slot machines means that they can have virtually any possible prize structure, including many small to medium prizes with rare huge jackpots.
With 516 stops on the virtual reel, the jackpot prize could be as rare as 1 in 137 million (1/5163), which means that the machine could safely offer progressive jackpot prizes as high as $20 million or $30 million and still make a profit in the long term. U.S. Patent #4,448,419 describes the logic of virtual reel mapping and can be found at http://www.uspto.gov/patft/index.html.
Because of virtual reel mapping, the odds of any picture coming up on a pay line are independent of the number of pictures on an actual reel. The reels simply display computer-determined outcomes. The computer tells the reel of pictures where to stop depending on the random selection from the virtual reel positions. The pictures do not determine what the slot machine will pay out or not; the computer determines where the pictures will stop and when to payout.
Inside a slot machine is a computer chip with tables of weights called virtual reels. The values generated by the RNG are used to select numbers on the virtual reels, which connect to specific pictures on the actual reels or video-displayed reels.
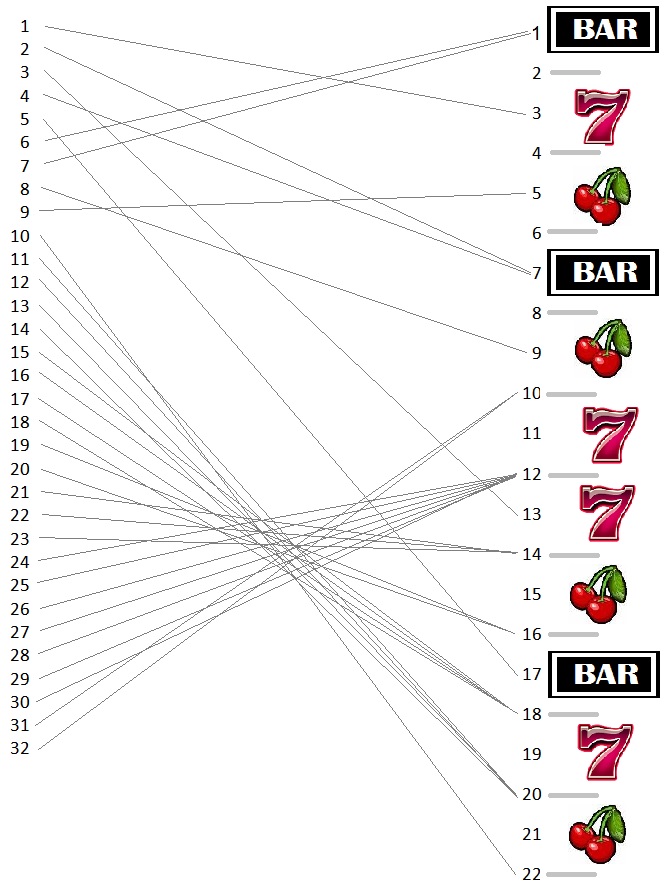
Each virtual reel has a specific number of stops: it could be 32, 64, or as many as 516. Some symbols are linked to a large number of stops; some are linked to very few. Some pictures might not be mapped to any number, meaning that the reel will never stop on that particular spot. The Safe@play slot machine tutorial gives an example of how the virtual reel is “mapped” to the actual reel on a mechanical slot machine (see above).
Note that there are only 9 virtual reel positions mapped to “winning” symbols on the actual reel and 20 virtual reel positions mapped to blanks.
Also, notice how virtual reel positions 24 to 30 map onto stop #12 on the actual reel. Stop #12 is a blank placed between two sevens. This particular figure might be a bit of an exaggeration. However, it clearly illustrates the manner in which virtual reel symbols are mapped onto the physical reel that is then seen by the player. On an actual slot machine, the bias toward nonwinning stops might be more subtle.
Virtual reel mapping applies specifically to three-reel slot machines. Five-reel video slots are so incredibly complex, with so many pay lines (up to nine crisscrossing), that it is difficult to see what advantage the casino would gain by using virtual reel weights. The five reels by themselves would give the game long enough odds to permit large jackpots. An anonymous reviewer, from the gaming industry, of an earlier draft of this article, told us that, with video slots, the player sees the virtual reel.
That is, with video slots, the pictures are not weighted. This is because the game’s designer is not limited by the circumference of a reel but can set the reel length at any arbitrary number of symbols.
Virtual reels are simply not needed on video slots. However, as with mechanical slots, trying to determine the size and symbol distribution on the video slots is quite difficult.
Casino Games Blog 2026
The Bitcoin Casino Guide
Was This Helpful?
Recommend us on Facebook